There’s been a lot of talk lately about how the presidential polls might be biased. So let’s look at how well – or poorly – some of the major survey firms are actually performing this year.
All polls contain error, mainly from the limitations of random sampling. But there are lots of other ways that error can creep into surveys. Pollsters who truly care about getting the right answer go through great pains to minimize these non-sampling errors, but sometimes systematic biases – or house effects – can remain. For whatever reason, some pollsters are consistently too favorable (or not favorable enough) to certain parties or candidates.
Since May 1, there have been over 400 state polls, conducted by more than 100 different survey organizations. However, a much smaller number of firms have been responsible for a majority of the polls: Rasmussen, PPP, YouGov, Quinnipiac, Purple Strategies, We Ask America, SurveyUSA, and Marist.
For each poll released by these firms, I’ll calculate the survey error as the difference between their reported level of support for Obama over Romney, and my model’s estimate of the “true” level of support on the day and state of the poll. Then each firm’s house effect is simply the average of these differences. (Note that my model doesn’t preemptively try to adjust for house effects in any way.) If a firm is unbiased, its average error should be zero. Positive house effects are more pro-Obama; negative house effects are more pro-Romney. Here’s what we find.
| Survey Firm | # Polls | House Effect |
| PPP | 61 | +0.7% |
| Marist | 15 | +0.5% |
| SurveyUSA | 22 | +0.3% |
| Quinnipiac | 35 | +0.1% |
| YouGov | 27 | 0% |
| We Ask America | 17 | -0.2% |
| Purple Strategies | 18 | -0.9% |
| Rasmussen | 53 | -0.9% |
There are a number of pieces of information to take away from this table. First, none of the house effects are all that big. Average deviations are less than 1% in either direction. This is much smaller than the error we observe in the polls due to random sampling alone.
Second, even if, say, Rasmussen is getting the right numbers on average – so that PPP’s house effect is actually +1.6% – then that +1.6% bias still isn’t that big. It’s certainly not enough to explain Obama’s large – and increasing – lead in the polls. Of course, it’s possible that even Rasmussen is biased pro-Obama, and we just aren’t able to tell. But I don’t believe anyone is suggesting that.
Finally, the firms with the largest house effects in both directions – PPP and Rasmussen – are also the ones doing the most polls, so their effects cancel out. Just another reason to feel comfortable trusting the polling averages.
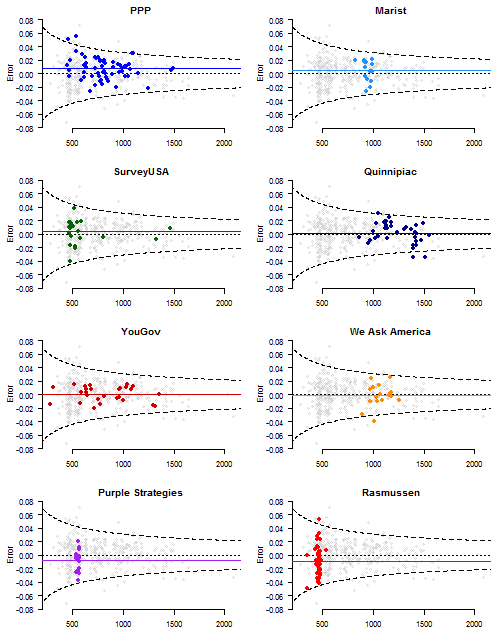
Here’s a plot highlighting each of the eight firms’ survey errors versus sample sizes. The horizontal lines denote the house effects. Dashed lines indicate theoretical 95% margins of error, assuming perfect random sampling. Again, nothing very extraordinary. We would expect PPP and Rasmussen to “miss” once or twice, simply because of how many polls they’re fielding.
Just out of curiosity (and no particular feelings of cruelty, I swear), which polls have been the most misleading – or let’s say, unluckiest – of the campaign so far? Rather than look at the raw survey error, which is expected to be larger in small samples, I’ll calculate the p-value for each poll, assuming my model represents the truth. This tells us the probability of getting a survey result with the observed level of error (or greater), at a given sample size, due to chance alone. Smaller p-values reveal more anomalous polls.
Here are all surveys with a p-value less than 0.01 – meaning we’d expect to see these results in fewer than 1 out of every 100 surveys, if the polling firm is conducting the survey in a proper and unbiased manner.
| p-value | Error | Survey Firm | Date | State | Obama | Romney | Sample Size |
| 0.001 | 0.07 | Suffolk | 9/16/2012 | MA | 64% | 31% | 600 |
| 0.002 | -0.07 | InsiderAdvantage | 9/18/2012 | GA | 35% | 56% | 483 |
| 0.003 | -0.03 | Gravis Marketing | 9/9/2012 | VA | 44% | 49% | 2238 |
| 0.003 | -0.05 | Wenzel Strategies (R) | 9/11/2012 | MO | 38% | 57% | 850 |
| 0.003 | 0.05 | Rutgers-Eagleton | 6/4/2012 | NJ | 56% | 33% | 1065 |
| 0.004 | -0.04 | FMWB (D) | 8/16/2012 | MI | 44% | 48% | 1733 |
| 0.005 | -0.05 | Gravis Marketing | 8/23/2012 | MO | 36% | 53% | 1057 |
| 0.006 | -0.03 | Quinnipiac | 5/21/2012 | FL | 41% | 47% | 1722 |
| 0.009 | -0.04 | Quinnipiac/NYT/CBS | 8/6/2012 | CO | 45% | 50% | 1463 |
The single most… unusual survey was the 9/16 Suffolk poll in Massachusetts that overestimated Obama’s level of support by 7%. However, of the nine polls on the list, seven erred in the direction of Romney – not Obama. And what to say about Gravis Marketing, who appears twice – strongly favoring Romney – despite only conducting 10 polls. Hm.
It’s interesting that many of these surveys had relatively large sample sizes. The result is that errors of only 3%-4% appear more suspicious than if the sample had been smaller. It’s sort of a double whammy: firms pay to conduct more interviews, but all they accomplish by reducing their sampling error is to provide sharper focus on the magnitude of their non-sampling error. They’d be better off sticking to samples of 500, where systematic errors wouldn’t be as apparent.

Drew, are you going to update for the 3rd estimate of GDP?
Yes – I’ll include it in the next update. Thanks for the heads up. I see the BEA revised Q2 GDP growth downward from 1.7% to 1.3%.
Hi Drew — great site.
Can you comment on how many polls you computed p-values for and the effect of multiple testing? I guess I am curious on whether the p-value of 0.001 is really significant, given that there were greater than 400 polls (I think) used for the data exploration here.
Not sure if I am doing this quite correctly, but I think for Hochberg’s procedure for multiplicity adjustment, it would be something like —
alpha = 0.05 (for example)
0.05/(400-1+1) = 0.000125, which is less than 0.001, so we fail to reject
0.05/(400-2+1) = 0.0001253, which is less than 0.002, so we fail to reject,
etc. etc.
So does this mean that the test of the hypothesis on each poll polls are due to random sampling does not have enough evidence to reject it?
David: I just computed the p-values for each poll assuming my model estimates represented the true value. It’s the probabilities I’m interested in. Since I’m not doing any significance testing or trying to reject a null hypothesis, there’s no need to correct for anything. With 400 state polls, we’d expect to see 4 or so on this list… I’ll let you decide what it means that there’s 9 (and that some firms appear more than once).
Is it possible to calculate if the error for polls from a given pollster vary with other variables? For instance, are some pollsters more or less skewed if the race in that state was close to even at the time of the poll? What about as a function of time before election day?